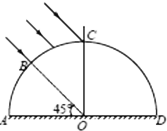
如图,横截面为半圆形的柱型玻璃砖,折射率为n=2,半圆的半径为R,底面AD涂有反射膜,一束平行光沿与底面成45°角方向射向玻璃砖的BC范围,OB与水平方向夹角为45°,C点在圆心O的正上方
问题描述:
如图,横截面为半圆形的柱型玻璃砖,折射率为n=| 2 |
 最佳答案:
最佳答案: 根据临界角公式sinC=
| 1 |
| n |
临界角 C=45°
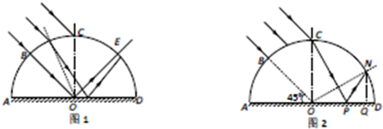
则沿BO射入的光,经反射后沿OE方向射出,E为弧CD的中点,从BC部分进入玻璃砖的光经反射后到达弧CD的光路,如图1所示.
从C点射入的光经P点反射后到达N点,此即为射出的光中在弧面上最靠近D处的点.
由折射定律 n=
| sini |
| sinr |
由几何关系可知,∠NPQ=60°
设∠NOD=α,由几何关系知:
ON•cosα-PNcos60°=OP
又 OP=OCtan30°
解得 α=30°
∠ONP=30°,所有从弧BC上进入的光能全部从弧面EN部分射出.EN之间的弧对应的圆心角为15°
弧长l=
| πR |
| 12 |
答:圆弧上有光射出的长度为
| πR |
| 12 |
版权声明
声明:有的资源均来自网络转载,版权归原作者所有,如有侵犯到您的权益
请联系本站我们将配合处理!
