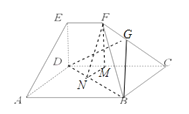
如图，在五面体ABCDEF中，四边形ABCD是矩形，DE⊥平面ABCD．

如图，在五面体ABCDEF中，四边形ABCD是矩形，DE⊥平面ABCD．

（Ⅰ）求证：AB∥EF；

（Ⅱ）若AB=BC=2EF=2，BD与平面BCF成30°的角，求二面角F﹣BD﹣C的正切值．

【答案】

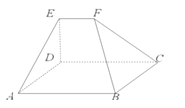
（Ⅰ）证明：∵AB∥CD，CD⊂面CDEF，AB⊄面CDEF，

∴AB∥面CDEF．

又∵AB⊂面ABEF，面ABEF∩面CDEF=EF，

∴AB∥EF；

（Ⅱ）解：∵DE⊥面ABCD，∴DE⊥BC．

又∵BC⊥CD，∴BC⊥面CDEF．

又∵BC⊂面BCF，∴面BCF⊥面CDEF．

过点D作DG⊥CF，则DG⊥面BCF，∴∠DBG为BD与平面BCF所成角．即∠DBG=30°

又BD=2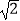，∴DG=BD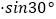=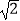，则DE=1且点G与点F重合．

取DC中点M，连接FM，则FM⊥面ABCD，

过M作MN⊥BD交BD于点N，连接FN，则∠FNM即为二面角F﹣BD﹣C的平面角，

∴tan=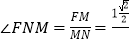

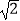
【解析】

（Ⅰ）由四边形ABCD是矩形，得到AB∥平面CDEF，由此能证明AB∥EF．

（Ⅱ）过点D作DG⊥CF，则DG⊥面BCF，可得∠DBG为BD与平面BCF所成角；取DC中点M，连接FM，则FM⊥面ABCD，过M作MN⊥BD交BD于点N，连接FN，则∠FNM即为二面角F﹣BD﹣C的平面角，即可求出二面角F﹣BD﹣C的正切值．

【考点精析】解答此题的关键在于理解空间中直线与直线之间的位置关系的相关知识，掌握相交直线：同一平面内，有且只有一个公共点；平行直线：同一平面内，没有公共点；异面直线： 不同在任何一个平面内，没有公共点．