设等比数列{an}的前n项和为Sn , a3=<img alt="1" src="/tk/20210512/1620750805543.png"/>
设等比数列{an}的前n项和为Sn , a3= , 且S2+
, 且S2+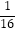 , S3 , S4成等差数列,数列{bn}满足bn=8n.求数列{an}的通项公式;
, S3 , S4成等差数列,数列{bn}满足bn=8n.求数列{an}的通项公式;
解:记数列{an}的公比为q,由S2+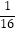 ,S3 , S4成等差数列,
,S3 , S4成等差数列,
可知2S3=S2+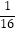 +S4 , 即a3=a4+
+S4 , 即a3=a4+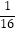 ,
,
又a3= ,故a4=
,故a4=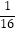 ,从而q=
,从而q=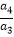 =
= ,
,
则a1=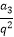 =
= ,an=
,an= x
x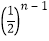 =
=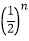 (n∈N*)
(n∈N*)
记数列{an}的公比为q,则2S3=S2+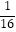 +S4 , 即a3=a4+
+S4 , 即a3=a4+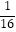 , 又由a3=
, 又由a3= , 知a4=
, 知a4=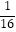 , 从而q=
, 从而q= , 根据公式即得结果.
, 根据公式即得结果.
【考点精析】关于本题考查的等比数列的通项公式(及其变式),需要了解通项公式: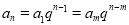 才能得出正确答案.
才能得出正确答案.
版权声明
声明:有的资源均来自网络转载,版权归原作者所有,如有侵犯到您的权益
请联系本站我们将配合处理!
