已知ai＞0（i=1，2，…，n），考查
①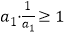
；
②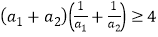
；
③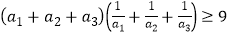
．
归纳出对a1 ， a2 ， …，an都成立的类似不等式，并用数学归纳法加以证明．
【答案】结论：（a1+a2+…+an）（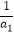
+
+…+
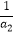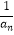）≥n2
证明：①当n=1时，显然成立；
②假设当n=k时，不等式成立，
即：（a1+a2+…+ak）（++…+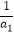
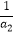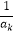）≥k2
那么，当n=k+1时，
（a1+a2+…+ak+ak+1）（++…++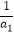
）
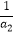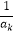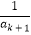=（a1+a2+…+ak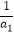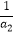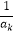）（++…+）+ak+1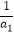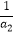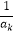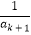（++…+）+（a1+a2+…+ak）+1
≥k2+（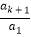
+
）+（
+
）+…+（
+
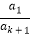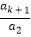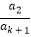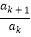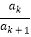）+1
≥k2+2k+1
=（k+1）2
即n=k+1时，不等式也成立．
由①②知，不等式对任意正整数n成立．
【解析】依题意可归纳出：（a1+a2+…+an）（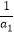
+
+…+
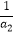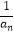）≥n2；下面用数学归纳法证明：①当n=1时易证；②假设当n=k时，不等式成立，去证明当n=k+1时，不等式也成立即可，需注意归纳假设的利用与基本不等式的应用．
版权声明
声明：有的资源均来自网络转载，版权归原作者所有，如有侵犯到您的权益
请联系本站我们将配合处理！