已知函数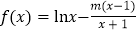 .
.
(1)若函数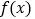 在定义域
在定义域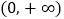 内单调递增,求实数
内单调递增,求实数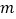 的取值范围;
的取值范围;
(2)对于任意的正实数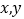 ,且
,且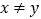 ,求证:
,求证: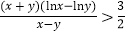 .
.
(1)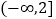 ;(2)见解析.
;(2)见解析.
(1)函数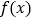 在定义域
在定义域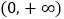 内单调递增,等价于
内单调递增,等价于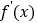
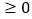 对于任意
对于任意 恒成立,即
恒成立,即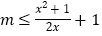 对于任意
对于任意 恒成立,利用基本不等式求出函数最小值,从而可得结果;(2)设
恒成立,利用基本不等式求出函数最小值,从而可得结果;(2)设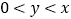 .令
.令 ,则
,则 ,原不等式等价于
,原不等式等价于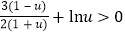 ,可证明
,可证明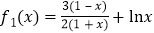 在
在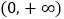 上递增.又因为
上递增.又因为 ,则
,则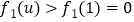 ,从而可得结论.
,从而可得结论.
(1)依题意,导数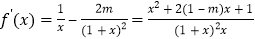
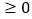 对于任意
对于任意 恒成立,即不等式
恒成立,即不等式
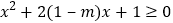 对于任意
对于任意 恒成立,即不等式
恒成立,即不等式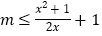 对于任意
对于任意 恒成立;
恒成立;
又因为当 时
时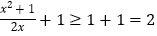 (当
(当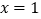 时取等号),则
时取等号),则 ,故实数
,故实数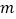 的取值范围是
的取值范围是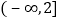 .
.
(2)由于目标不等式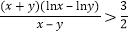 中两个字母
中两个字母 与
与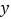 可以轮换,则不妨设
可以轮换,则不妨设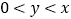 .令
.令 ,则
,则 .
.
欲证目标不等式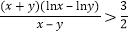
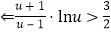
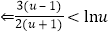
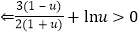 . (※)
. (※)
根据(1)的结论知,当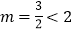 时
时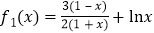 在
在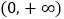 上递增.又因为
上递增.又因为 ,则
,则
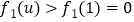 ,则不等式(※)正确,故原目标不等式得证.
,则不等式(※)正确,故原目标不等式得证.
版权声明
声明:有的资源均来自网络转载,版权归原作者所有,如有侵犯到您的权益
请联系本站我们将配合处理!
