直线<img alt="1" src="/tk/20210512/1620768248925.png"/>与x轴,y轴分别交于A,B两点,点A关于直
直线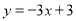 与x轴,y轴分别交于A,B两点,点A关于直线
与x轴,y轴分别交于A,B两点,点A关于直线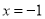 的对称点为点C.
的对称点为点C.
(1)求点C的坐标;
(2)若抛物线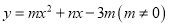 经过A,B,C三点,求该抛物线的表达式;
经过A,B,C三点,求该抛物线的表达式;
(3)若抛物线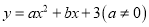 经过A,B两点,且顶点在第二象限,抛物线与线段AC有两个公共点,求a的取值范围.
经过A,B两点,且顶点在第二象限,抛物线与线段AC有两个公共点,求a的取值范围.
(1)点C的坐标(﹣3,0);
(2)抛物线的表达式为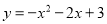 ;
;
(3)a的取值范围是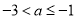
(1)把y=0,代入函数解析式,求出点A的坐标,根据对称得出C点的坐标即可;(2)先求出B点坐标,再把点A、B三点的坐标分别代入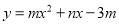 ,解得m、n的值即可;(3)根据题意抛物线开口向下,所以当图像经过A点的关于原点对称的点时a取最大值,当经过点C时开口最大,a的值最小.
,解得m、n的值即可;(3)根据题意抛物线开口向下,所以当图像经过A点的关于原点对称的点时a取最大值,当经过点C时开口最大,a的值最小.
解:(1)令y=0,得x=1.
∴点A的坐标为(1,0).
∵点A关于直线x=﹣1对称点为点C,
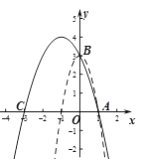
∴点C的坐标为(﹣3,0).
(2)令x=0,得y=3.
∴点B的坐标为(0,3).
∵抛物线经过点B,
∴﹣3m=3,解得m=﹣1.
∵抛物线经过点A,
∴m+n﹣3m=0,解得n=﹣2.
∴抛物线表达式为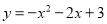 .
.
(3)由题意可知,a<0.
根据抛物线的对称性,当抛物线经过(﹣1,0)时,开口最小,a=﹣3,
此时抛物线顶点在y轴上,不符合题意.
当抛物线经过(﹣3,0)时,开口最大,a=﹣1.
结合函数图像可知,a的取值范围为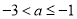 .
.
版权声明
声明:有的资源均来自网络转载,版权归原作者所有,如有侵犯到您的权益
请联系本站我们将配合处理!
