如图所示,半径为R=1m的圆弧形轨道固定在水平轨道上,与弧形轨道相切的水平轨道上静置一小球B,小球A从弧形轨道上离水平地面高度h=0.8m处由静止释放后,沿轨道下滑与小球B发生碰撞并粘在一起。所有接触
如图所示,半径为R=1m的圆弧形轨道固定在水平轨道上,与弧形轨道相切的水平轨道上静置一小球B,小球A从弧形轨道上离水平地面高度h=0.8m处由静止释放后,沿轨道下滑与小球B发生碰撞并粘在一起。所有接触面觉光滑,A、B两球的质量均为m=1kg,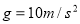 ,求:
,求:

(1)小球A在弧形轨道最低点时对轨道的压力大小为F;
(2)小球A、B碰撞过程中损失的机械能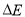 。
。
(1)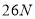 (2)
(2)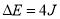
(1)小球A在光滑弧形轨道上下滑时,由机械能守恒定律,得: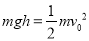
可得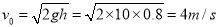
在弧形轨道最低点时,由牛顿第二定律得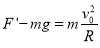 ,解得
,解得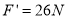 根据牛顿第三定律得,小球对轨道的压力大小
根据牛顿第三定律得,小球对轨道的压力大小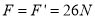
(2)取水平向右为正方向,A与B碰撞的过程中动量守恒,由动量守恒定律有:
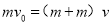 ,得v=2m/s
,得v=2m/s
由能量守恒定律得: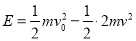
代入数据得:△E=4J
版权声明
声明:有的资源均来自网络转载,版权归原作者所有,如有侵犯到您的权益
请联系本站我们将配合处理!
