如图所示，足够长的粗糙斜面与水平面成θ=37°放置，在斜面上虚线aa＇和bb＇与斜面底边平行，且间距为d=0.1m，在<img alt="1" src="/tk/2

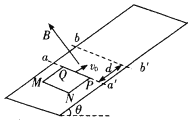
如图所示，足够长的粗糙斜面与水平面成θ=37°放置，在斜面上虚线aa＇和bb＇与斜面底边平行，且间距为d=0.1m，在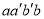围成的区域有垂直斜面向上的有界匀强磁场，磁感应强度为B=1T；现有一质量为m=10g，总电阻为R=1Ω，边长也为d=0.1m的正方形金属线圈MN-PQ，其初始位置PQ边与aa＇重合，现让金属线圈以一定初速度沿斜面向上运动，当金属线圈从最高点返回到磁场区域时，线圈刚好做匀速直线运动．已知线圈与斜面间的动摩擦因数为μ=0.5，不计其它阻力（取sin37°=0.6，cos37°=0.8，g=10m/s2）求：

（1）线圈向下返回到磁场区域时的速度；

（2）线圈向上离开磁场区域时的动能；

（3）线圈向下通过磁场过程中，线圈电阻R上产生的焦耳热．

【答案】

（1）2m/s；（2）0.1J；（3）0.004J

【解析】

（1）线框进入磁场时，产生的感应电动势：E=Bdv

电流：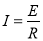

安培力：F=BId

线框做匀速直线运动，由平衡条件得：mgsinθ=μmgcosθ+F

解得：v=2m/s；

（2）线圈离开磁场最高点的距离为x，线圈离开磁场最高点时，

由动能定理得：-mgxsinθ-μmgxcosθ=0-EK1，

线圈从最高点进入磁场时，由动能定理得：mgxsinθ-μmgxcosθ=EK-0

其中：EK=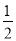mv2，

解得：EK1=0.1J；

（3）线圈向下匀速通过磁场过程中，由能量守恒定律得：

mg•2dsinθ-μmg•2dcosθ+W=0

焦耳热：Q=-W

解得：Q=0.004J；