如图，在⊙O直径AB的延长线上任取一点C，过点C做直线CE与⊙O交于点D、E，在⊙O上取一点F，使<img alt="1" src="/tk/20210512/16

如图，在⊙O直径AB的延长线上任取一点C，过点C做直线CE与⊙O交于点D、E，在⊙O上取一点F，使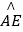= 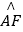， 连接DF，交AB于G．

（1）求证：E、D、G、O四点共圆；

（2）若CB=OB，求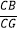的值．

【答案】

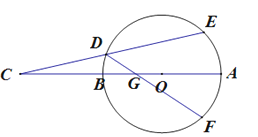
（1）证明：∵∠EDF的度数等于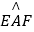的度数的一半，而=，

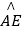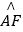∴∠EDF的度数等于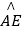的度数．

∵∠AOF的度数等于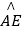的度数，

∴∠EDF=∠AOE，

∵∠COE与∠AOE互补，

∴∠COE与∠EDF互补，

∴E、D、G、O四点共圆；

（2）解：由（Ⅰ）知E、D、G、O四点共圆，

∴CE•CD=CO•CG，

∵CE•CD=CA•CB，

∴CA•CB=CO•CG，

∵CB=OB，

∴==．

【解析】

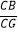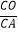（1）证明∠EDF=∠AOE，利用∠COE与∠AOE互补，可得∠COE与∠EDF互补，从而可得E、D、G、O四点共圆；

（2）利用四点共圆，结合割线定理，即可求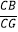的值．