已知函数f（x）=ax2﹣<img alt="1" src="/tk/20210512/1620750802150.png"/>x+2ln（x+1）

已知函数f（x）=ax2﹣x+2ln（x+1）

（Ⅰ）求函数f（x）的图象在点（0，f（0））的切线方程；

（Ⅱ）设函数h（x）=f（x）﹣ln（x+1），当x∈[0，+∞）时，h（x）≤x恒成立，求实数a的取值范围．

【答案】

解：（Ⅰ）f（0）=0，所以切点为（0，0），

∵f′（x）=2ax﹣+，

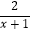∴f′（0）=﹣+2=，

∴所求切线方程为y=x，

（Ⅱ）由题设，当x∈[0，+∞）时，不等式ax2+ln（x+1）﹣x≤0恒成立，

设g（x）=ax2+ln（x+1）﹣x，（x≥0），只需g（x）max≤0即可，

由g′（x）=2ax+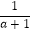﹣1=，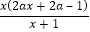

（1）当a=0时，g′（x）=﹣，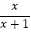

当x＞0时，g′（x）＜0，函数g（x）在[0，+∞）上单调递减，

故g（x）max=g（0）=0，满足条件，

（2）当a＞0时，令g′（x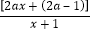）==0，解得x=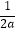﹣1，

①若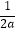﹣1≤0，即a≥，在区间（0，+∞）上，g′（x）＞0，

则函数g（x）在[0，+∞）上单调递增，g（x）≥0，当且仅当x=0时等号成立，此时不满足条件，

②若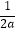﹣1＞0，即0＜a＜时，函数g（x）在（0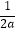，﹣1）上单调递减，在区间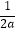（﹣1，+∞）上单调递增，

g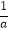（）=lg（1+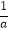）＞0，此时不满足条件，

（3）当a＜0时，由g′（x）=，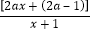

∴2ax+（2a﹣1）＜1，

∴g′（x）＜0，函数g（x）在[0，+∞）上单调递减，

故g（x）max=g（0）=0，满足条件，

综上所述，实数a的取值范围为（﹣∞，0]

【解析】

（Ⅰ）根据导数的几何意义即可求出．

（Ⅱ）若对任意的x∈[0，+∞），h（x）≤x恒成立，则f（x）﹣g（x）≤0恒成立，g（x）=ax2+ln（x+1）﹣x，（x≥0），只需g（x）max≤0，分类讨论后，综合讨论结果可得实数a的取值范围．

【考点精析】本题主要考查了函数的最大(小)值与导数的相关知识点，需要掌握求函数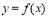在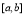上的最大值与最小值的步骤：（1）求函数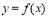在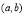内的极值；（2）将函数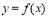的各极值与端点处的函数值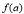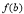，比较，其中最大的是一个最大值，最小的是最小值才能正确解答此题．