三个顶点均在椭圆上的三角形称为椭圆的内解三角形．已知<img alt="1" src="/tk/20210512/1620752143055.png"/&
三个顶点均在椭圆上的三角形称为椭圆的内解三角形．已知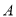
为椭圆
（
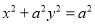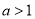）的上顶点，若以
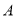为直角顶点的等腰直角三角形
有且只有三解，则椭圆的离心率的取值范围是__________．
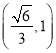
由题意可设：直线AB的方程为y=kx+1，（k＞0），直线AC的方程为y=﹣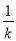
x+1，
联立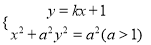
，化为：（1+a2k2）x2+2ka2x=0，解得xB=-
,
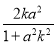yB=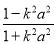
,|AB|=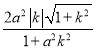
同理可得：x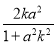C=
，yC=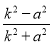
|AC|=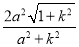
∵|AB|=|AC|，
∴
=
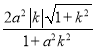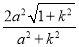
化为：a2（k2﹣k）=k3﹣1，
当k=1时是其中一个根．
当k≠1时，a2=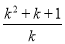
=k+
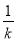+1＞3，
∴1＞e=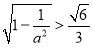
故答案为：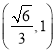
．
版权声明
声明：有的资源均来自网络转载，版权归原作者所有，如有侵犯到您的权益
请联系本站我们将配合处理！