已知单调递增的等比数列{an}满足：a2+a3+a4=28，且a3+2是a2、a4的等差中项．

已知单调递增的等比数列{an}满足：a2+a3+a4=28，且a3+2是a2、a4的等差中项．

（Ⅰ）求数列{an}的通项公式；

（Ⅱ）若bn=anlog2an ， Sn=b1+b2+…+bn ， 求数列{bn}的前n项和Sn ．

【答案】

解：（Ⅰ）设等比数列{an}的首项为a1 ， 公比为q，

∵a3+2是a2、a4的等差中项，

∴2（a3+2）=a2+a4 ．

代入a2+a3+a4=28，得a3=8．

∴，

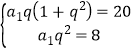解之得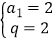：或，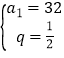

又∵{an}单调递增，

∴，

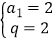∴an=2n ．

（Ⅱ）由（1）知，bn=anlog2an=n•2n ．

∴Sn=2+2×22+3×23+…+n•2n ，

2Sn=22+2×23+3×24+…+（n﹣1）•2n+n•2n+1 ，

∴﹣Sn=2+22+…+2n﹣n•2n+1=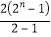﹣n•2n+1=（1﹣n）•2n+1﹣2，

∴Sn=（n﹣1）•2n+1+2．

【解析】

（Ⅰ）设等比数列{an}的首项为a1 ， 公比为q，由于a3+2是a2、a4的等差中项，可得2（a3+2）=a2+a4 ． 代入a2+a3+a4=28，得a3 ． 再利用等比数列的通项公式即可得出．

（II）由（1）知，bn=anlog2an=n•2n ． 再利用“错位相减法”与等比数列的前n项和公式即可得出．

【考点精析】本题主要考查了数列的前n项和和数列的通项公式的相关知识点，需要掌握数列{an}的前n项和sn与通项an的关系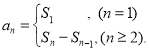；如果数列an的第n项与n之间的关系可以用一个公式表示，那么这个公式就叫这个数列的通项公式才能正确解答此题．