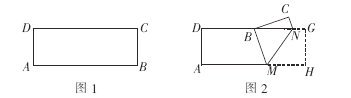
如图1,2在矩形纸片ABCD中,AD=6,AB=9.点M,N分别在AB,DC上(M不与A,B重合,N不与C,D重合),现以MN为折痕,将矩形纸片ABCD折叠.
如图1,2在矩形纸片ABCD中,AD=6,AB=9.点M,N分别在AB,DC上(M不与A,B重合,N不与C,D重合),现以MN为折痕,将矩形纸片ABCD折叠.
(1)当B 点落在DC上时(如图2),求证:△MNB是等腰三角形;
(2)当B点与D点重合时,试求△MNB的面积;
(3)当B点与AD的中点重合时,试求折痕MN的长.
(1)证明见解析;(2)S△MNB=19.5;(3)MN=2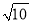 .
.
(1)先判断出AM∥DN,进而得出∠BNM=∠BMN=∠NMH,即可得出结论;
(2)先根据勾股定理求出DN,再用三角形得面积公式即可得出结论;
(3)先根据勾股定理求出BH,再判断出△ABH∽△EMN即可得出结论.
(1)如答图1,
∵四边形AHGD是矩形 ,
∴AM∥DN,
∴∠BNM=∠BMN=∠MNH,
∴△MNB是等腰三角形.;
(2)如答图2,当点B与点D重合时,
设MB=MF=x,则AM=9-x,
由勾股定理得:62+(9-x)2=x2,解得x=6.5,
∴MD=ND=6.5,
∴S△MNB=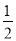 ×6×6.5=19.5.
×6×6.5=19.5.
(3)如答图3,当点B与AD的中点重合时,连接BH交MN于点F,过点N作NE⊥AH于点E,
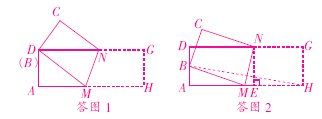
∵AD=6,
∴AB=DB=3,
∴BH2=32+92.
∴BH=3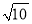 .
.
∵NM垂直平分HB,NE⊥AH,
∴∠MNE=∠AHB.
∵∠A=∠NEM,
∴△ABH~△AHB.
∴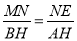 .
.
∴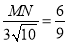 .
.
∴MN=2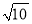 .
.
版权声明
声明:有的资源均来自网络转载,版权归原作者所有,如有侵犯到您的权益
请联系本站我们将配合处理!
