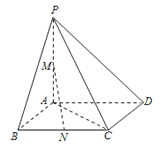
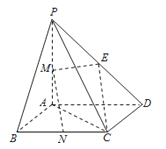
如图，四棱锥P﹣ABCD中，PA=AB=1，PA⊥底面ABCD，底面ABCD为正方形，且M，N分别为PA与BC的中点

如图，四棱锥P﹣ABCD中，PA=AB=1，PA⊥底面ABCD，底面ABCD为正方形，且M，N分别为PA与BC的中点

（1）求证：CD⊥平面PAD

（2）求证：MN∥平面PCD．

【答案】

证明：（1）∵PA⊥平面ABCD，

∴PA⊥CD，

∵四边形ABCD是正方形，∴AD⊥CD，

∴CD⊥平面PAD…3分

（2）取PD的中点E，连接ME，CE，

∵M，N分别为PA，BC的中点，

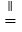
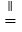
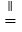∴MEAD，NCAD，∴MENC

∴MNCE是平行四边形，∴MN∥CE，

∵CE⊆平面PCD，MN⊄平面PCD，

∴MN∥平面PCD．

【解析】

（1）有题意可证明PA⊥CD，AD⊥CD，从而可证明CD⊥平面PAD．

（2）取PD的中点E，连接ME，CE，可证明MN∥CE，由于CE⊆平面PCD，MN⊄平面PCD，即可得证MN∥平面PCD．

【考点精析】本题主要考查了直线与平面平行的判定和直线与平面垂直的判定的相关知识点，需要掌握平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行；一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直；注意点：a)定理中的“两条相交直线”这一条件不可忽视；b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想才能正确解答此题．