设函数f（x）=x（ex﹣1）+ax2

设函数f（x）=x（ex﹣1）+ax2

（Ⅰ）当a=﹣时，求f（x）的单调区间；

（Ⅱ）若当x≥0时，f（x）≥0恒成立，求a的取值范围．

【答案】

解：（1）当a=-时，，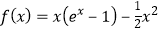

f'（x）=（ex﹣1）+xex﹣x=（x+1）（ex﹣1）

令f'（x）＞0，得x＜﹣1或x＞0；

令f'（x）＜0，得﹣1＜x＜0

所以f（x）的单增区间为（﹣∞，﹣1），（0，+∞）；单减区间为（﹣1，0）

（2）f（x）=x（ex﹣1）+ax2=x（ex﹣1+ax），

令g（x）=（ex﹣1+ax），x∈[0，+∞），

g'（x）=ex+a，g（0）=0…

当a≥﹣1时，g'（x）=ex+a＞0，g（x）在[0，+∞）上为增函数，

而g（0）=0，从而当x≥0时，f（x）≥0恒成立．

当a＜﹣1时，令g'（x）=ex+a=0，得x=ln（﹣a）．

当x∈（0，ln（﹣a））时，g'（x）＜0，

g（x）在（0，ln（﹣a））上是减函数，

而g（0）=0，从而当x∈（0，ln（﹣a））时，g（x）＜0，即f（x）＜0

综上，a的取值范围是[﹣1，+∞）

【解析】

（1）当a=-时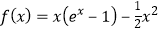， ， 由此利用导数性质能求出f（x）的单调区间．

（2）f（x）=x（ex﹣1）+ax2=x（ex﹣1+ax），令g（x）=（ex﹣1+ax），x∈[0，+∞），由此利用导数性质能求出a的取值范围．

【考点精析】认真审题，首先需要了解函数的最大(小)值与导数(求函数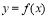在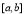上的最大值与最小值的步骤：（1）求函数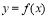在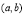内的极值；（2）将函数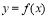的各极值与端点处的函数值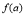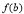，比较，其中最大的是一个最大值，最小的是最小值)．