已知函数f（x）=2<img alt="1" src="/tk/20210512/1620750873040.png"/>sinxcosx﹣3sin

已知函数f（x）=2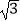sinxcosx﹣3sin2x﹣cos2x+2．

（1）当x∈[0，]时，求f（x）的值域；

（2）若△ABC的内角A，B，C的对边分别为a，b，c，且满足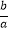= 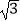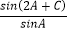， =2+2cos（A+C），求f（B）的值．

【答案】

解：（1）∵f（x）=2sinxcosx﹣3sin2x﹣cos2x+2

=sin2x﹣2sin2x+1

=sin2x+cos2x

=2sin（2x+）

∵x∈[0，]，

∴2x+∈[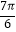，]，sin（2x+）∈[﹣，1]，

∴f（x）∈[﹣1，2]…6分

（2）∵由题意可得sin[A+（A+C）]=2sinA+2sinAcos（A+C）

有，sinAcos（A+C）+cosAsin（A+C）=2sinA+2sinAcos（A+C）

化简可得：sinC=2sinA，

∴由正弦定理可得：c=2a，

∵b=a，

∴由余弦定理可得：cosA===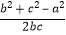

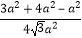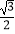
∴可解得：A=30°，B=60°，C=90°

所以可得：f（B）=1

【解析】

（1）由三角函数中的恒等变换应用化简函数解析式可得f（x）=2sin（2x+）．由x∈[0，]，可得sin（2x+）∈[﹣ ， 1]，从而解得f（x）的值域；

（2）由题意根据三角函数中的恒等变换应用可得sinC=2sinA，由正弦定理可得c=2a，又b=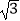a，由余弦定理可解得A的值，从而求得B，C的值，即可求得f（B）的值．