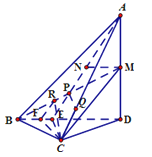
如图,在四面体A﹣BCD中,AD⊥平面BCD,BC⊥CD,CD=2,AD=4.M是AD的中点,P是BM的中点,点Q在线段AC上,且AQ=3QC.
如图,在四面体A﹣BCD中,AD⊥平面BCD,BC⊥CD,CD=2,AD=4.M是AD的中点,P是BM的中点,点Q在线段AC上,且AQ=3QC.
(1)证明:PQ∥平面BCD;
(2)若异面直线PQ与CD所成的角为45°,二面角C﹣BM﹣D的大小为θ,求cosθ的值.
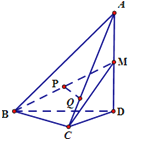
(1)证明:如图,连AP并延长交BD于E,连CE,
过M作MN∥BD交AP于N,则AN=NE,NP=PE.
故AP=3PE,从而PQ∥CE.
因PQ⊄平面BCD,CE⊂平面BCD,
故PQ∥平面BCD.
(2)解:过C作CF⊥BD于F,作CR⊥BM于R,连FR.
因AD⊥平面BCD,故平面ABD⊥平面BCD,
故CF⊥平面ABD,因此CF⊥BM,从而BM⊥平面RCF,
所以∠CRF=θ即为二面角C﹣BM﹣D的平面角.
因PQ∥CE,故∠DCE=45°,因此CE即为∠BCD的角平分线.
由 (1)知DE=2MN=2EB,故DC=2BC,
从而BC=1,CF=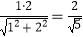 .
.
由题意知BC⊥平面ACD,故BC⊥CM.
由题意知CM=2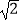 ,故CR=
,故CR=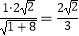 .
.
所以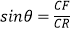 =
=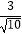 ,从而
,从而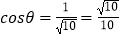 .
.
(1)连AP并延长交BD于E,连CE,过M作MN∥BD交AP于N,由已知条件推导出PQ∥CE.由此能证明PQ∥平面BCD.
(2)过C作CF⊥BD于F,作CR⊥BM于R,连FR.由已知条件推导出∠CRF=θ即为二面角C﹣BM﹣D的平面角,由此能求出cosθ的值.
【考点精析】根据题目的已知条件,利用异面直线及其所成的角的相关知识可以得到问题的答案,需要掌握异面直线所成角的求法:1、平移法:在异面直线中的一条直线中选择一特殊点,作另一条的平行线;2、补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系.
版权声明
声明:有的资源均来自网络转载,版权归原作者所有,如有侵犯到您的权益
请联系本站我们将配合处理!
