数列{an}的前n项和为Sn ． 且点（n，Sn）在函数f（x）=3x2﹣2x的图象上．

数列{an}的前n项和为Sn ． 且点（n，Sn）在函数f（x）=3x2﹣2x的图象上．

（1）求数列{an} 的通项公式；

（2）设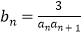 ， Tn是数列{bn}的前n项和，求使得Tn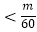对所有的n∈N*都成立的最小值m．

【答案】

解：（1）∵点（n，Sn）在函数f（x）=3x2﹣2x的图象上

∴Sn=3n2﹣2n，

当n≥2时，an=sn﹣sn﹣1=6n﹣5

当n=1时，也符合上式

∴an=6n﹣5；

（2）由（1）得=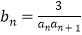

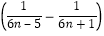
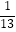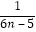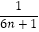故Tn=（1﹣+﹣+…+﹣）=（1﹣）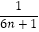

因此，要使Tn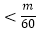对所有的n∈N*都成立，只需使得（1﹣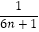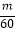）＜（n∈N*）成立的m，必须且仅须满足m≥30，所以满足要求的最小值m为30．

【解析】

（1）首先根据条件得出Sn=3n2﹣2n，然后利用an=sn﹣sn﹣1求出通项公式；

（2）由（1）得出数列{bn}的通项公式，利用裂项法求和，即可求使得Tn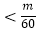对所有的n∈N*都成立的最小值m．