已知函数f(x)=ax﹣2lnx,a∈R
(Ⅰ)当a=3时,求函数在(1,f(1))的切线方程
(Ⅱ)求函数f(x)的极值.
【答案】x
(0,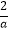 )
)
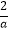
(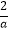 ,+
,+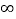 )
)
f'(x)
﹣
0
+
f(x)
单调递减
极小值
单调递增
∴当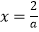 时,f(x)取得极小值f(
时,f(x)取得极小值f(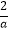 )=2-2ln
)=2-2ln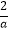 ,综上,当a≤0时,f(x)没有极值;当a>0时,f(x)的极小值为2-2ln
,综上,当a≤0时,f(x)没有极值;当a>0时,f(x)的极小值为2-2ln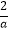 ,没有极大值.
,没有极大值.
(Ⅰ)把a=3代入函数解析式并求出导数,求出f′(1)和f(1),代入点斜式方程化简即可得到切线方程;
(Ⅱ)求出原函数的导函数和定义域,分a≤0和a>0讨论,分别由导函数的符号判断出函数单调区间,并求出函数的极值.
【考点精析】本题主要考查了函数的极值与导数的相关知识点,需要掌握求函数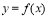 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在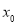 附近的左侧
附近的左侧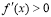 ,右侧
,右侧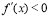 ,那么
,那么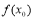 是极大值(2)如果在
是极大值(2)如果在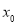 附近的左侧
附近的左侧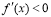 ,右侧
,右侧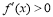 ,那么
,那么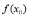 是极小值才能正确解答此题.
是极小值才能正确解答此题.
版权声明
声明:有的资源均来自网络转载,版权归原作者所有,如有侵犯到您的权益
请联系本站我们将配合处理!
