已知函数f(x)=x3+ax2+b(a,b∈R)
(1)若函数f(x)在x=0,x=2处取得极值,且极小值为﹣2,求a,b的值.
(2)若x∈[0,1],函数f(x)在图象上任意一点的切线的斜率为k,求k≤1恒成立时a的取值范围.
【答案】解:(1)由f'(x)=3x2+2ax得x=0或x=-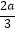
∴-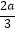 =2得a=﹣3.
=2得a=﹣3.
当0<x<2时,f'(x)<0,当x>2时f'(x)>0
故当x=2时f(x)取得极小值,f(2)=8+4a+b=﹣2
所以b=2…(6分)
(2)当x∈[0,1],k=f'(x)=3x2+2ax≤1恒成立,
即令g(x)=3x2+2ax﹣1≤0对一切x∈[0,1]恒成立,
只需 即a≤﹣1
即a≤﹣1
所以a的取值范围为(﹣∞,﹣1]
【解析】(1)通过求函数的导数,函数f(x)在x=0,x=2处取得极值,就是x=0,x=2时导数为0,求出a,利用极小值为﹣2,求出b;
(2)由(1)可得f(x)的解析式.x∈[0,1],函数f(x)图象上的任意一点的切线斜率为k,k≤1恒成立,就是导函数的值域≤1恒成立,再用二次函数根与系数的关系,求实数a的取值范围.
【考点精析】掌握函数的极值与导数是解答本题的根本,需要知道求函数 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在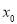 附近的左侧
附近的左侧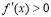 ,右侧
,右侧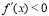 ,那么
,那么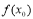 是极大值(2)如果在
是极大值(2)如果在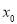 附近的左侧
附近的左侧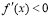 ,右侧
,右侧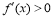 ,那么
,那么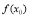 是极小值.
是极小值.
版权声明
声明:有的资源均来自网络转载,版权归原作者所有,如有侵犯到您的权益
请联系本站我们将配合处理!
