已知函数f(x)=(x2+ax+a)ex(a≤2,x∈R)
(1)若a=1,求y=f(x)在点(0,f(0))处的切线方程;
(2)是否存在实数a,使得f(x)的极大值为3,若存在,求出a的值;若不存在,说明理由.
【答案】x
(﹣∞,﹣2)
﹣2
(﹣2,﹣a)
﹣a
(﹣a,+∞)
f′(x)
+
0
﹣
0
+
f(x)
递增
极大
递减
极小
递增
则当x=﹣2时,函数取得极大值f(﹣2),由f(﹣2)=3得a=4﹣3e2 . 故存在a=4﹣3e2 .
【解析】(1)求函数的导数,利用导数的几何意义即可求y=f(x)在点(0,f(0))处的切线方程;
(2)求函数的导数,根据函数的极值和导数的关系求出函数的极大值,进行判断.
【考点精析】关于本题考查的函数的极值与导数,需要了解求函数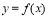 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在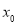 附近的左侧
附近的左侧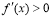 ,右侧
,右侧 ,那么
,那么 是极大值(2)如果在
是极大值(2)如果在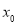 附近的左侧
附近的左侧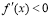 ,右侧
,右侧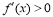 ,那么
,那么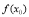 是极小值才能得出正确答案.
是极小值才能得出正确答案.
版权声明
声明:有的资源均来自网络转载,版权归原作者所有,如有侵犯到您的权益
请联系本站我们将配合处理!
上一篇 : 已知函数f(x)=ax﹣2lnx,a∈R
下一篇 :返回列表
